Son dönemde sosyal medyada viral olan resimde kaç üçgen var temalı bir soru büyük ilgi uyandırdı. Sorunun çözümü ise tek tek saymaktan değil kombinasyon yapabilmekten geçiyor.
Po-Shen Loh, Cornell Üniversitesi’nden bir matematikçi ve ilginç bir sorunun da mucidi. Cornell, hiçbiri paralel olmayan 6 çizgi çektiği ve hiçbir noktada ikiden fazla çizginin kesişmediği ilginç bir soru hazırlayarak görüntüde kaç üçgen olduğunu sordu.
Bu problem, geçtiğimiz günlerde gündeme gelen ve tartışma yaratan 8/2(2+2) sorusunun aksine saf matematik içeriyor ancak oldukça ilginç ve karmaşık bir çözüm yoluna sahip.
Soruda altı tane doğru var ve bu doğruların hiçbiri paralel değil. Hiçbir noktada 2’den fazla doğru kesişmiyor. Buradaki meydan okuma, doğru hesaplama yöntemini bulmaktan geçiyor. Yani doğru cevabı parmakla sayarak bulduysanız bir ehemmiyeti yok.
Sorunun cevabı için Dr. Loh’un bir de ipucu var: Bir üçgen üç doğrudan oluşur. Yani 6 çizgim varsa, soru bunlardan 3’ünü kaç farklı şekilde seçebilirim haline geliyor.
Twitter’da ve çeşitli mecralarda pek çok kullanıcı, kombinasyon konusunu iyi öğrendikleri için anında cevap vermiş oldu. Diğerleri saymaya çalıştıysa da Dr. Loh, neredeyse hiç doğru sayan birine rastlamadığını söylüyor.

Bu soruda ilk olarak her üç çizginin yalnızca bir üçgen oluşturacağı gerçeğine dikkat etmek gerekiyor. Yani B, C ve E doğruları yalnızca tek bir üçgen oluşturur.
Öncelikle 6 doğrudan üç tanesini rastgele seçtiğimiz durumları ele alalım. Elimizde 6 doğru var. Birini seçtik geriye 5 kaldı. Onu da kenara ayırıp son doğrumuzu seçmeye karar verdiğimizde elimizde 4 alternatif kalmış oluyor. Bu durumda farklı alternatif sayımız 6x5x4=120 çıkıyor. Şimdi herkes resimde 120 üçgen olmadığını söylüyor. Doğru, çünkü bu 120 sayısında aynı üçgenler farklı sıralamalar ile tekrar tekrar sayılıyor.
Doğrularımızı isimlendirmek gerekirse elimizde A, B, C, D, E, F doğruları var. Biz bunlardan üçünü, örneğin A, C, E’yi seçtik diyelim. ACE üçgeni ile ECA üçgeni aynı üçgendir. İlk yöntemde ACE, ECA, CAE, AEC, CEA, EAC üçgenleri tekrar tekrar sayıldı. Halbuki bu altı üçgen de aynı üçgendir. Her üçgen altı kere sayılmıştır.
Permütasyon yaparken yapılması gereken işlem, 6’nın 3’lüsünü almak olarak bilinen işlemdir. Yani 6’dan geriye doğru, altı da dahil 3 sayının çarpımının ilk üç sayının çarpımına bölünmesidir. Bu da bize (6x5x4)/(3.2.1) sonucunu verir. Haliyle işlem sonucu 120/6=20 çıkar. Yukarıda her üçgenin 6 kere sayıldığını söylemiştik.
Matematiğin gücü, karmaşık ve zor görünmesine rağmen burada yatıyor. Bir defa doğru yöntemi öğrendiğinizde artık işlem kolaylaşıyor. Resimde 6 değil de 96 çizgi olsa yine işlemi yapmak çok kısa sürecekti. (Cevap: (96x95x94)/(3.2.1)= 142880)
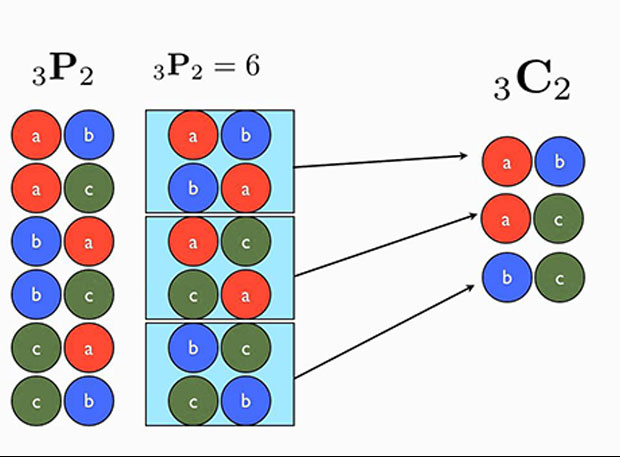
Kombinasyon sorularının tamamı özünde aynıdır ve benzer bir şekilde çözülür. Farklı renklerde altı topu bir torbaya attığınızda, sıralamaları fark etmeksizin kaç farklı renk kombinasyonuyla 3 top çekebilirsiniz? O da aynı yöntemle çözülüyor, cevap 20.
Gelelim renklerin, harflerin ya da rakamların aynı olduğu duruma. Bu yöntem bol bol faktöriyel, yani ! işaretinden önceki tüm pozitif tam sayıların çarpımı işlemini içeriyor. (2!= 2.1, 5!= 5.4.3.2.1 gibi) Diyelim ki kutuda 3 sarı 2 kırmızı top var. Alt tarafa hemen 3! ve 2! de ekliyoruz, çünkü topların hangisinin çıktığı önemli değil, toplar özdeş. Bu durum sık sık karşımıza ADANADAN sözcüğündeki harfler kullanılarak, anlamlı ya da anlamsız kaç farklı 4 harfli sözcük yazılabilir ya da 843343 sayısının rakamlarıyla kaç farklı 3 basamaklı sayı yazılabilir sorularında da kullanılır.
Dr. Loh’un sorusunun cevabı özünde C(6,3)’ün çözümüdür. Bu da matematiksel olarak 6!/(3!3!) demektir. Zira kombinasyon sorularında temel formül, n toplam birim sayısı, r çekilen/seçilen birim sayısı olacak şekilde C(n,r) = n!/((n-r)!r! şeklinde yazılır. (Bizdeki matematik eğitiminde, işlemi kolaylaştırmak için ilk üç sayı ile baştaki 3 faktöriyel işleme sokulur çünkü iki tarafta da olan çarpanlar sadeleşecektir.)
Matematiksel sorular ve denklemler, birbirleriyle benzer şekillerde çözülür. Bu da matematiğin bir güzelliği olarak ortaya çıkar.
Kaynak
Po-Shen Loh, Cornell Üniversitesi’nden bir matematikçi ve ilginç bir sorunun da mucidi. Cornell, hiçbiri paralel olmayan 6 çizgi çektiği ve hiçbir noktada ikiden fazla çizginin kesişmediği ilginç bir soru hazırlayarak görüntüde kaç üçgen olduğunu sordu.
Bu problem, geçtiğimiz günlerde gündeme gelen ve tartışma yaratan 8/2(2+2) sorusunun aksine saf matematik içeriyor ancak oldukça ilginç ve karmaşık bir çözüm yoluna sahip.
Soruda altı tane doğru var ve bu doğruların hiçbiri paralel değil. Hiçbir noktada 2’den fazla doğru kesişmiyor. Buradaki meydan okuma, doğru hesaplama yöntemini bulmaktan geçiyor. Yani doğru cevabı parmakla sayarak bulduysanız bir ehemmiyeti yok.
Sorunun cevabı için Dr. Loh’un bir de ipucu var: Bir üçgen üç doğrudan oluşur. Yani 6 çizgim varsa, soru bunlardan 3’ünü kaç farklı şekilde seçebilirim haline geliyor.
Twitter’da ve çeşitli mecralarda pek çok kullanıcı, kombinasyon konusunu iyi öğrendikleri için anında cevap vermiş oldu. Diğerleri saymaya çalıştıysa da Dr. Loh, neredeyse hiç doğru sayan birine rastlamadığını söylüyor.

Bu soruda ilk olarak her üç çizginin yalnızca bir üçgen oluşturacağı gerçeğine dikkat etmek gerekiyor. Yani B, C ve E doğruları yalnızca tek bir üçgen oluşturur.
Öncelikle 6 doğrudan üç tanesini rastgele seçtiğimiz durumları ele alalım. Elimizde 6 doğru var. Birini seçtik geriye 5 kaldı. Onu da kenara ayırıp son doğrumuzu seçmeye karar verdiğimizde elimizde 4 alternatif kalmış oluyor. Bu durumda farklı alternatif sayımız 6x5x4=120 çıkıyor. Şimdi herkes resimde 120 üçgen olmadığını söylüyor. Doğru, çünkü bu 120 sayısında aynı üçgenler farklı sıralamalar ile tekrar tekrar sayılıyor.
Doğrularımızı isimlendirmek gerekirse elimizde A, B, C, D, E, F doğruları var. Biz bunlardan üçünü, örneğin A, C, E’yi seçtik diyelim. ACE üçgeni ile ECA üçgeni aynı üçgendir. İlk yöntemde ACE, ECA, CAE, AEC, CEA, EAC üçgenleri tekrar tekrar sayıldı. Halbuki bu altı üçgen de aynı üçgendir. Her üçgen altı kere sayılmıştır.
Permütasyon yaparken yapılması gereken işlem, 6’nın 3’lüsünü almak olarak bilinen işlemdir. Yani 6’dan geriye doğru, altı da dahil 3 sayının çarpımının ilk üç sayının çarpımına bölünmesidir. Bu da bize (6x5x4)/(3.2.1) sonucunu verir. Haliyle işlem sonucu 120/6=20 çıkar. Yukarıda her üçgenin 6 kere sayıldığını söylemiştik.
Matematiğin gücü, karmaşık ve zor görünmesine rağmen burada yatıyor. Bir defa doğru yöntemi öğrendiğinizde artık işlem kolaylaşıyor. Resimde 6 değil de 96 çizgi olsa yine işlemi yapmak çok kısa sürecekti. (Cevap: (96x95x94)/(3.2.1)= 142880)

Kombinasyon sorularının tamamı özünde aynıdır ve benzer bir şekilde çözülür. Farklı renklerde altı topu bir torbaya attığınızda, sıralamaları fark etmeksizin kaç farklı renk kombinasyonuyla 3 top çekebilirsiniz? O da aynı yöntemle çözülüyor, cevap 20.
Gelelim renklerin, harflerin ya da rakamların aynı olduğu duruma. Bu yöntem bol bol faktöriyel, yani ! işaretinden önceki tüm pozitif tam sayıların çarpımı işlemini içeriyor. (2!= 2.1, 5!= 5.4.3.2.1 gibi) Diyelim ki kutuda 3 sarı 2 kırmızı top var. Alt tarafa hemen 3! ve 2! de ekliyoruz, çünkü topların hangisinin çıktığı önemli değil, toplar özdeş. Bu durum sık sık karşımıza ADANADAN sözcüğündeki harfler kullanılarak, anlamlı ya da anlamsız kaç farklı 4 harfli sözcük yazılabilir ya da 843343 sayısının rakamlarıyla kaç farklı 3 basamaklı sayı yazılabilir sorularında da kullanılır.
Dr. Loh’un sorusunun cevabı özünde C(6,3)’ün çözümüdür. Bu da matematiksel olarak 6!/(3!3!) demektir. Zira kombinasyon sorularında temel formül, n toplam birim sayısı, r çekilen/seçilen birim sayısı olacak şekilde C(n,r) = n!/((n-r)!r! şeklinde yazılır. (Bizdeki matematik eğitiminde, işlemi kolaylaştırmak için ilk üç sayı ile baştaki 3 faktöriyel işleme sokulur çünkü iki tarafta da olan çarpanlar sadeleşecektir.)
Matematiksel sorular ve denklemler, birbirleriyle benzer şekillerde çözülür. Bu da matematiğin bir güzelliği olarak ortaya çıkar.
Kaynak

 Öğrenci Kariyeri
Öğrenci Kariyeri






 Sıla Tanrıverdi
Sıla Tanrıverdi





0 Yorum
Yorum Yap